机器学习(Machine Learning)
一、机器学习的第一性原理(Principles)
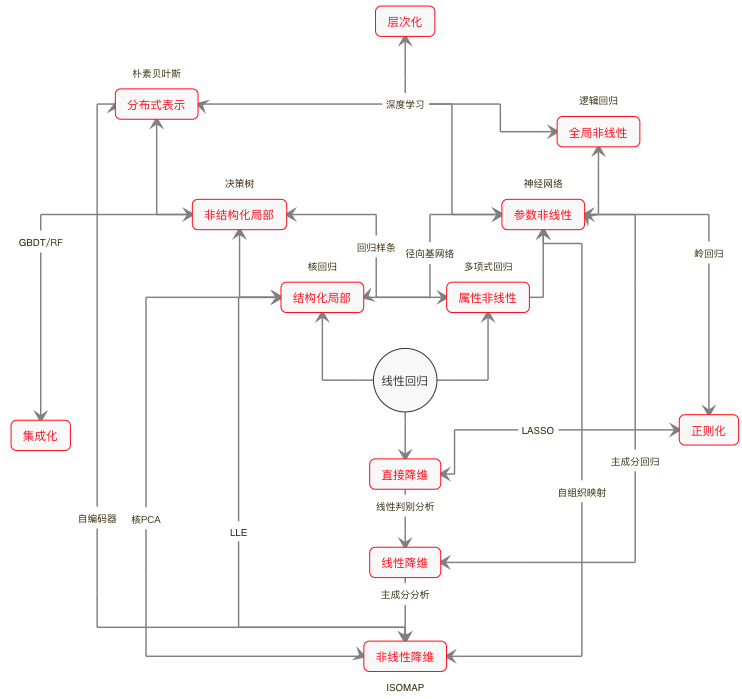
1.1 学习的本质定义
机器学习的本质:
在不完全信息条件下,利用有限样本,对未知决策函数进行近似,并在未来数据上保持稳定表现。
这一过程可抽象为:
现实世界 ↓(采样)数据分布 ↓(假设空间)模型族 ↓(优化)参数 ↓(决策)预测 / 行为三大永恒矛盾:
- 拟合能力 vs 泛化能力
- 表达能力 vs 稳定性
- 不确定性数据 vs 确定性决策
1.2 频率学派与贝叶斯学派
频率视角
- 参数是**固定但未知的常量**
- 数据是随机变量
- 学习目标:**经验风险最小化(ERM)**
用训练数据的经验分布近似真实分布,通过优化损失函数估计参数
贝叶斯视角
- 参数本身是**随机变量**
- 数据是已观测事实
- 学习结果是**参数的后验分布**
本质区别:是否显式建模不确定性
1.3 什么问题适合机器学习
机器学习适用问题需同时满足:
- 问题中存在可学习的模式(显性或隐性)
- 难以通过确定性规则精确建模
- 拥有足够规模与质量的数据
二、学习范式与方法体系(Methodologies)
2.1 学习范式总览
| 范式 | 核心目标 | 本质描述 |
|---|---|---|
| 监督学习 | 预测 | 从样本到标签的函数逼近 |
| 无监督学习 | 描述 | 发现数据内在结构 |
| 强化学习 | 决策 | 延迟奖励下的最优控制 |
| 迁移学习 | 复用 | 跨任务知识迁移 |
2.2 监督与无监督学习
- **监督学习**:直接逼近 $f(x) \to y$
- **无监督学习**:学习 $p(x)$ 或其结构
二者本质区别在于:是否存在明确的监督信号
2.3 集成学习:降低不确定性的系统方法
集成学习的核心哲学:通过多样性对抗不确定性
能力结构
集成学习├── 多样性来源│ ├── 数据扰动(Bagging)│ ├── 样本权重(Boosting)│ └── 模型异构(Stacking)├── 偏差-方差权衡├── 鲁棒性提升└── 工程代价方法分类
- **Bagging**:通过数据扰动降低方差
- **Boosting**:通过序列依赖降低偏差
- **Stacking**:通过元模型融合不同假设空间
AdaBoost
强分类器形式:
$$f(x)=\sum_{i=1}^n\alpha_iG_i(x)$$
本质:逐步聚焦“难样本”,重塑数据分布
三、模型、假设空间与复杂度(Models)
3.1 参数模型 vs 非参数模型
| 维度 | 参数模型 | 非参数模型 |
|---|---|---|
| 表达能力 | 有限 | 随数据增长 |
| 可解释性 | 强 | 弱 |
| 偏差 | 较高 | 较低 |
| 方差 | 较低 | 较高 |
本质区别:假设空间容量是否随数据增长
3.2 模型生命周期
- 模型拟合(训练集)
- 模型选择(验证集)
- 模型评估(测试集)
三者必须严格隔离,否则评估失真
四、优化:从搜索到逼近(Optimization)
4.1 优化的本质
优化不是“找最优解”,而是在巨大搜索空间中高效逼近可接受解
4.2 梯度下降的几何直觉
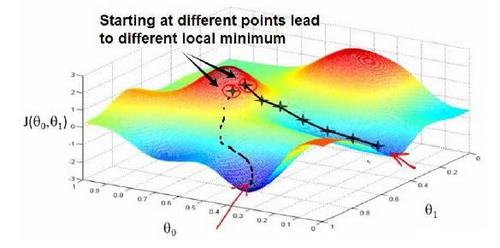
- 利用局部线性近似
- 沿负梯度方向迭代更新
$$w := w - \alpha \nabla J(w)$$
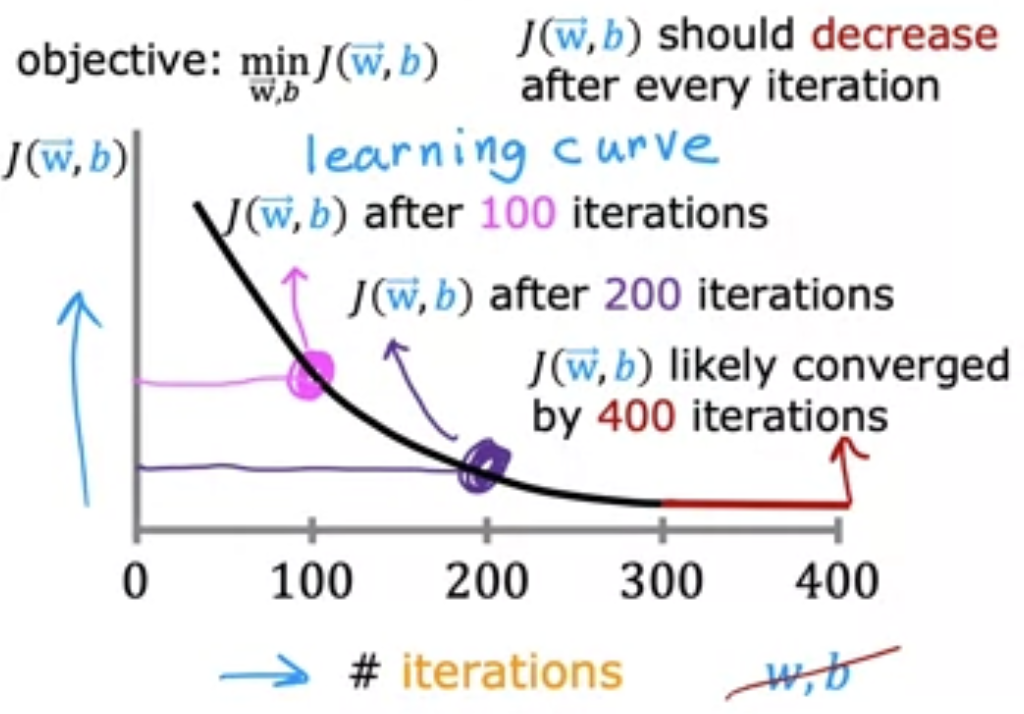
工程稳定性技巧
- 学习率控制
- 特征缩放
- 小批量梯度下降
- 软更新
4.3 随机化优化方法谱系
| 方法 | 核心思想 |
|---|---|
| 随机搜索 | 空间采样 |
| 爬山法 | 局部改进 |
| 模拟退火 | 接受劣解逃逸 |
| 遗传算法 | 群体进化 |
随机性用于对抗局部最优
五、泛化、过拟合与正则化(Generalization)
5.1 偏差-方差分解
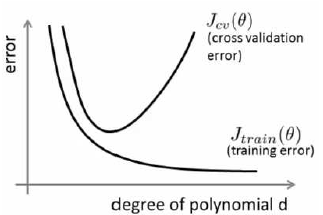
- 偏差:模型假设过强
- 方差:模型过于灵活
5.2 正则化的统一解释
正则化的本质:对函数空间施加约束
形式:
$$J = Loss + \lambda \cdot Complexity$$
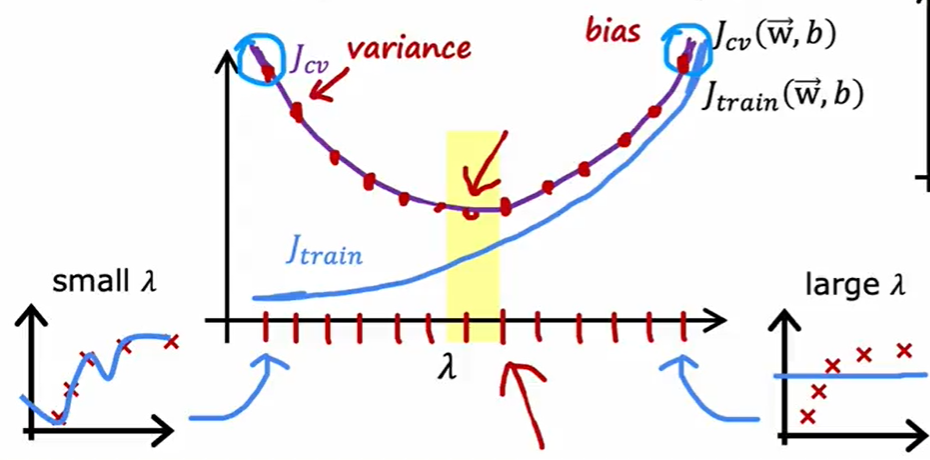
- L1:结构稀疏化
- L2:参数平滑化
5.3 学习曲线与数据规模
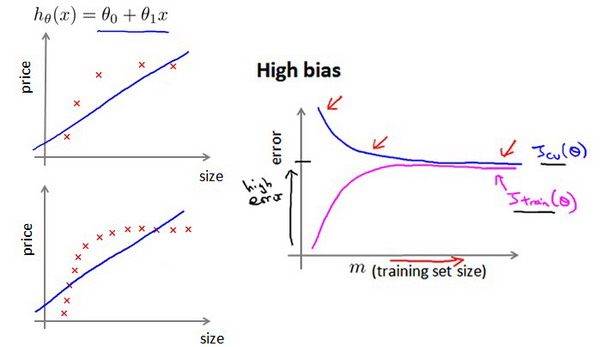
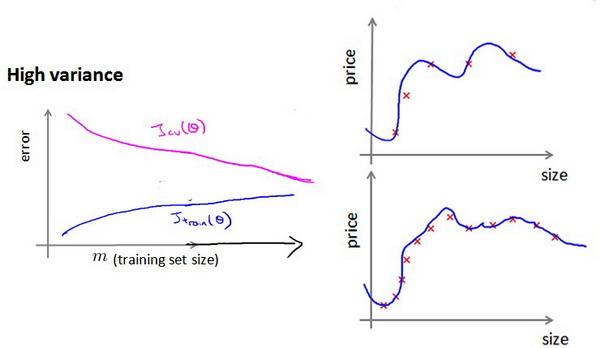
数据并非万能,错误的模型结构无法被数据拯救
六、实验设计与评估体系(Evaluation)
6.1 实验的工程哲学
实验的目的不是“证明模型好”,而是理解模型行为
- 控制变量
- 全因子实验
- 连续实验
6.2 数据划分策略
- Holdout
- 交叉验证
- 自助法
- 时间切割
- 离线 Replay
6.3 评估指标体系
- Accuracy / Precision / Recall
- F-Score
- ROC / AUC
- LogLoss
- RMSE
指标选择应服从业务风险偏好
七、强化学习:延迟奖励下的学习(RL)
强化学习解决的是:序列决策与长期回报最大化
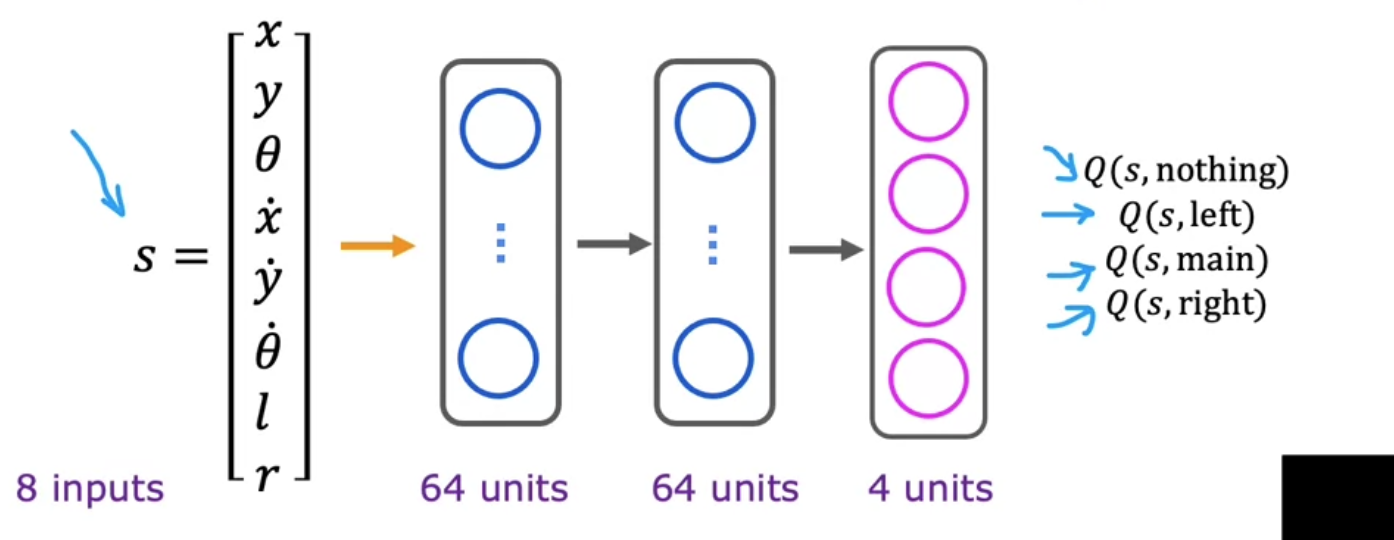
7.1 核心抽象
- 状态 $S$
- 动作 $A$
- 奖励 $R$
- 策略 $\pi$
7.2 贝尔曼方程
$$Q(s,a)=R(s)+\gamma\max_{a'}Q(s',a')$$
本质:递归定义最优性
八、概率图模型:结构化不确定性
8.1 建模哲学
用图结构表达随机变量之间的条件独立性
stateDiagram-v2a --> ca --> bb --> db --> cc --> e$$p(A,B,C,D,E)=p(A)p(B|A)p(C|A,B)p(D|B)p(E|C)$$
九、从算法到系统(ML as a System)
9.1 机器学习系统生命周期
数据 → 特征 → 模型 → 决策 → 反馈 → 再训练9.2 系统性挑战
- 数据漂移
- 概念漂移
- 评估失效
- 线上线下一致性
十、总结:机器学习的长期视角
机器学习不是"找到一个好算法",而是构建一个能够持续学习、纠错和进化的系统。
真正稳定的能力来自:
- 对不确定性的敬畏
- 对复杂度的克制
- 对系统行为的持续观测
关联内容(自动生成)
- [/数据技术/监督学习.html](/数据技术/监督学习.html) 监督学习是机器学习的重要范式之一,与文档中提到的监督学习概念密切相关
- [/数据技术/非监督学习.html](/数据技术/非监督学习.html) 非监督学习是机器学习的另一个重要范式,与文档中提到的无监督学习概念相对应
- [/数据技术/深度学习.html](/数据技术/深度学习.html) 深度学习是机器学习的一个重要分支,体现了文档中提到的模型复杂度与表达能力的关系
- [/数据技术/特征工程.html](/数据技术/特征工程.html) 特征工程是机器学习实践中重要的环节,直接影响模型的学习效果和泛化能力
- [/数据技术/推荐系统.html](/数据技术/推荐系统.html) 推荐系统是机器学习的重要应用领域,体现了文档中提到的从算法到系统的转化
- [/数据技术/数据分析.html](/数据技术/数据分析.html) 数据分析与机器学习密切相关,机器学习往往作为数据分析的高级手段
- [/数据技术/数据建模.html](/数据技术/数据建模.html) 数据建模是机器学习的基础,涉及文档中提到的假设空间和模型选择问题
- [/数据技术/数据处理.html](/数据技术/数据处理.html) 数据处理是机器学习流程中的重要环节,影响数据质量从而影响学习效果